GeoMat

Buy Now
Download latest version »
Description sheet (PDF)
User's manual (PDF)

The program is aimed at the solution under static loading of two classes of problems encountered in structural engineering: a soil-supported mat or a soil-supported structural slab. The mat or structural slab is modeled with linear finite elements. The shape may be rectangular, round, or irregular and the thickness may vary.

For the soil-supported mat, the soil is assumed to have a linear response which is defined with the subgrade modulus and is characterized by a set of springs which can vary in stiffness at points under the mat. The springs can reflect horizontal as well as vertical resistances. The solution follows the classical Winkler model. This method of modeling soil has been widely used in the analysis of flexible beams and mats on elastic materials.

Since the Winkler model, often referred to as a “one-parameter model”, cannot represent a continuous medium well, the modified Vlasov model by Vallabhan and Das (1988) was also introduced in GeoMat for solving the soil-structure interaction in continuous medium. The user will enter soil Young’s modulus and Poisson’s ratio of each sublayer instead of subgrade modulus underneath the foundation when using the modified Vlasov model which has improved the accuracy of the solution computed based on the Winkler soil model.


Gallery

Available commonly used structural sections
Contour
Flexural Bending Moment Along a Cutting Line
Loads from anchor bolts on circular pile-supported mat
Modeling Pile-Raft behavior by using soil springs and pile springs
Moment contour in pile-raft
shear contour in pile-raft
Various boundary and loading conditions

Methodology

The engineer must make several initial steps in performing the analysis and design of a soil-supported mat or a structural slab:

Assuming that a geotechnical engineer has provided information on the soil, leading to an estimate of the bearing capacity of the mat, the experience of the structural engineer will allow for the sizing of the mat or slab for the initial analyses.

With regard to the soil-supported mat, the initial data provided by the geotechnical engineer may show a range of values because settlement and differential movement are difficult to estimate since the settlement is dependent on the stiffness of the soil and on the rigidity of the mat.

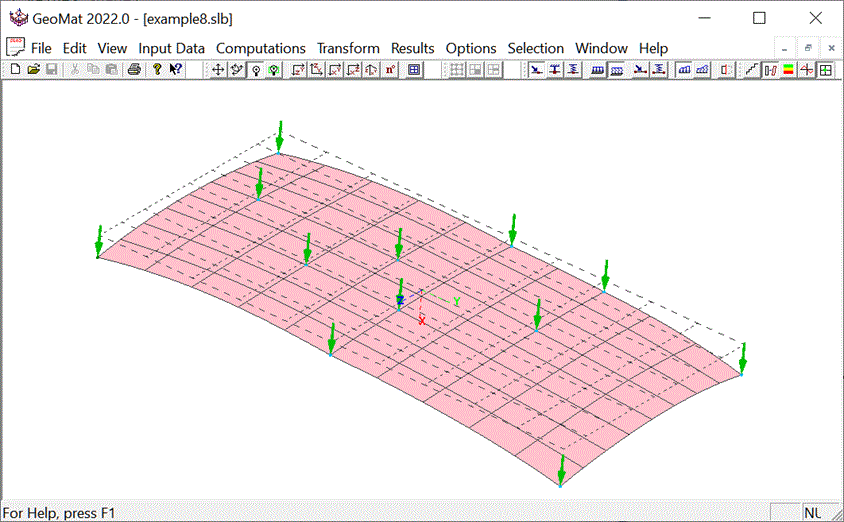
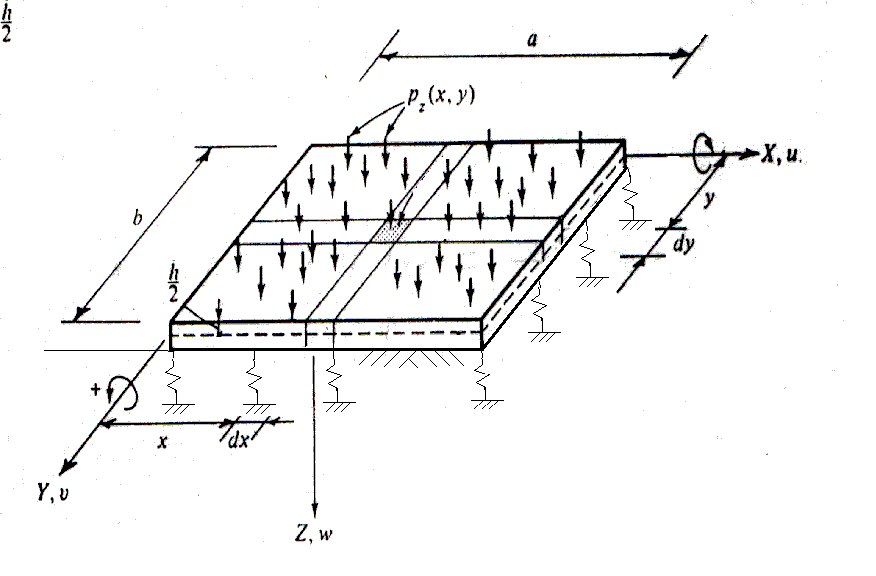
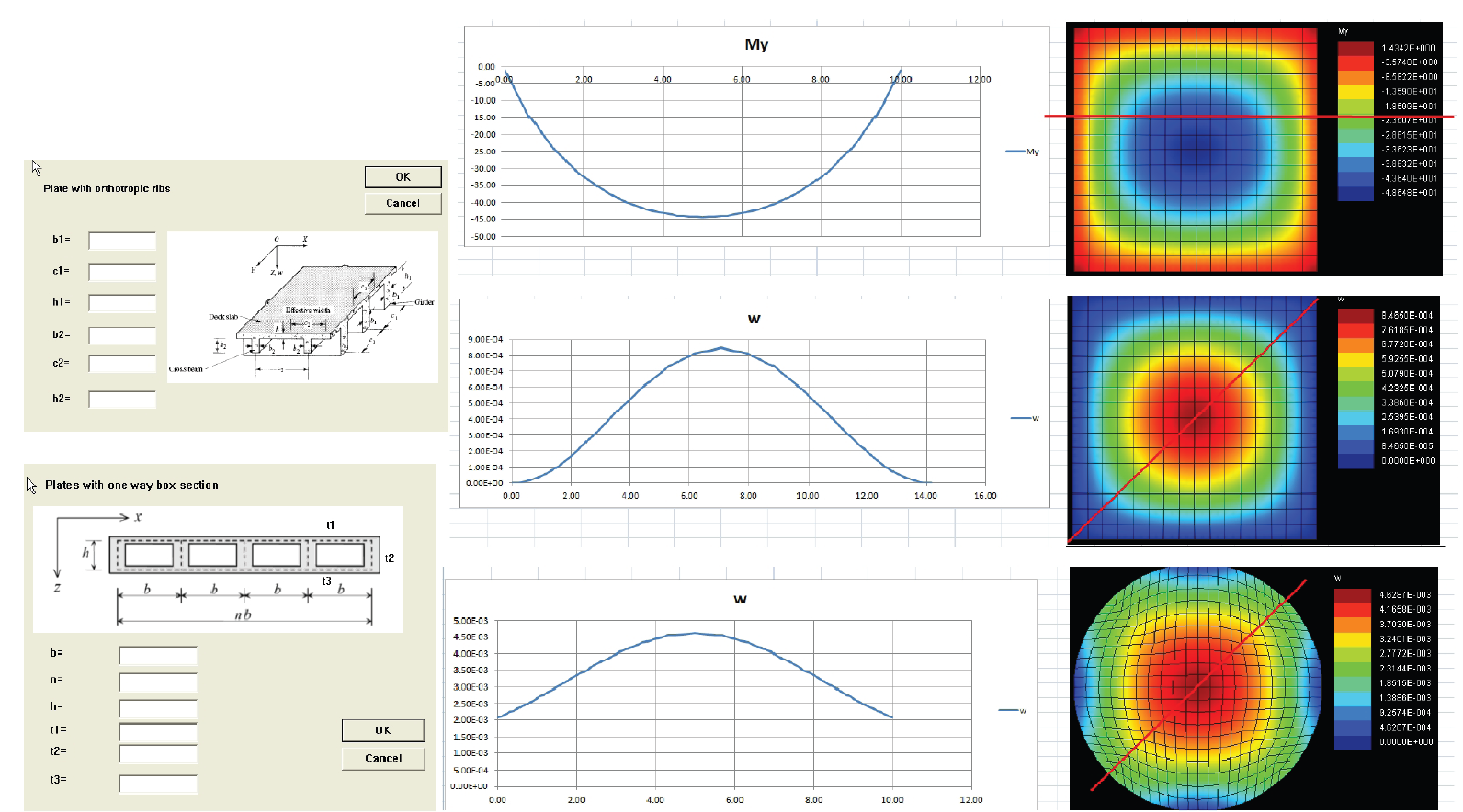
Loadings on a mat or a slab can vary widely in nature and magnitude. The finite-element method has been the best tool to take into account the variety of loadings as well as the properties of the material in a structure. With modern methods of characterizing material in the mat or slab and with the capability of current processors, the solutions to finite-element arrays proceed rapidly and with a degree of accuracy in the control of the user.

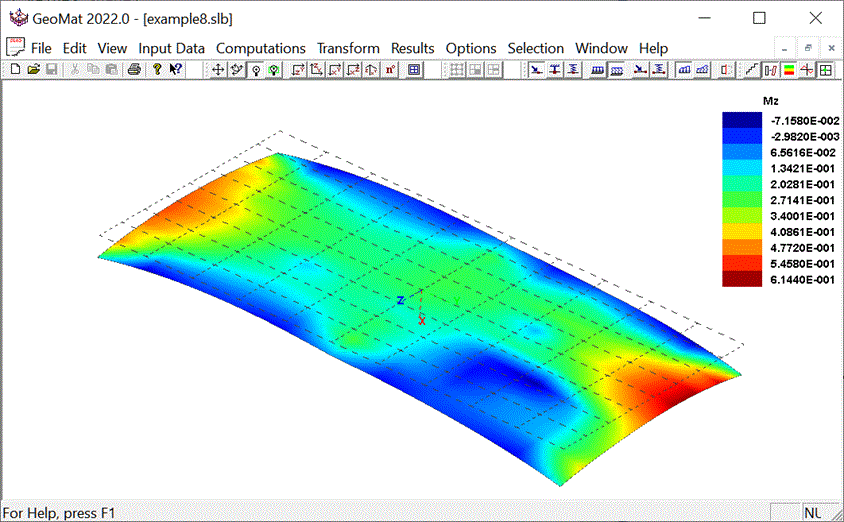
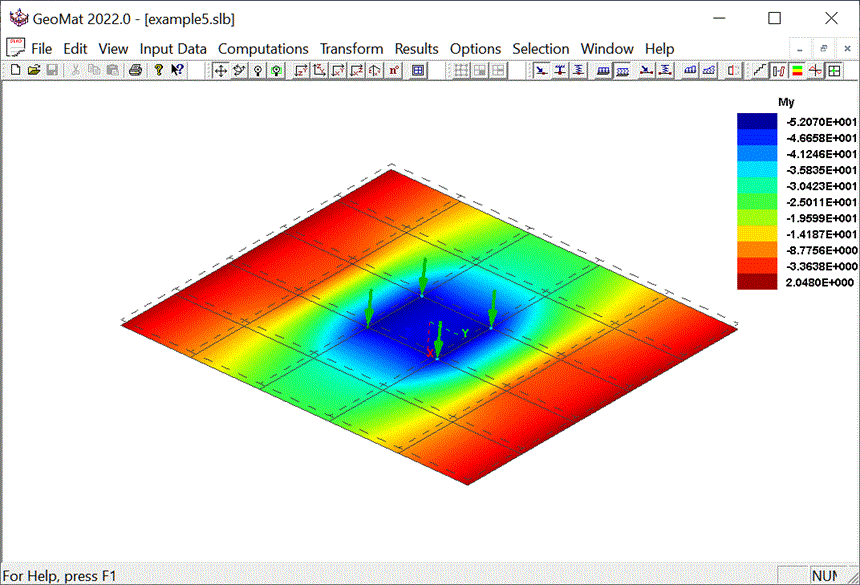
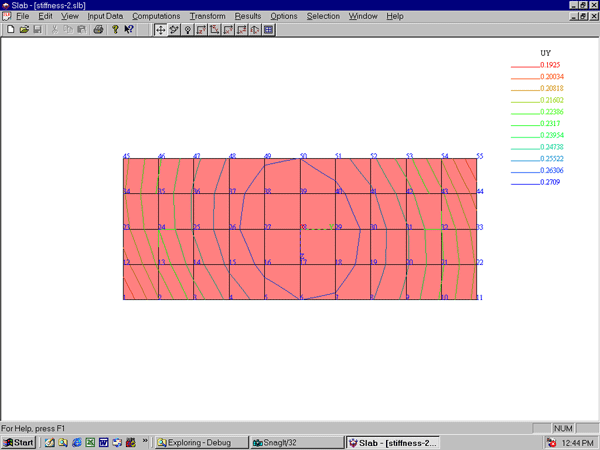
For a given set of loadings, deformations and movements within the mat and slab can be computed along with bending moment and shear stress at any point with the material. These results provide the engineer with information on which to base the design of the system. The method can be applied to a mat or slab that is circular, rectangular, or an irregular shape, leading to a powerful analytical tool.

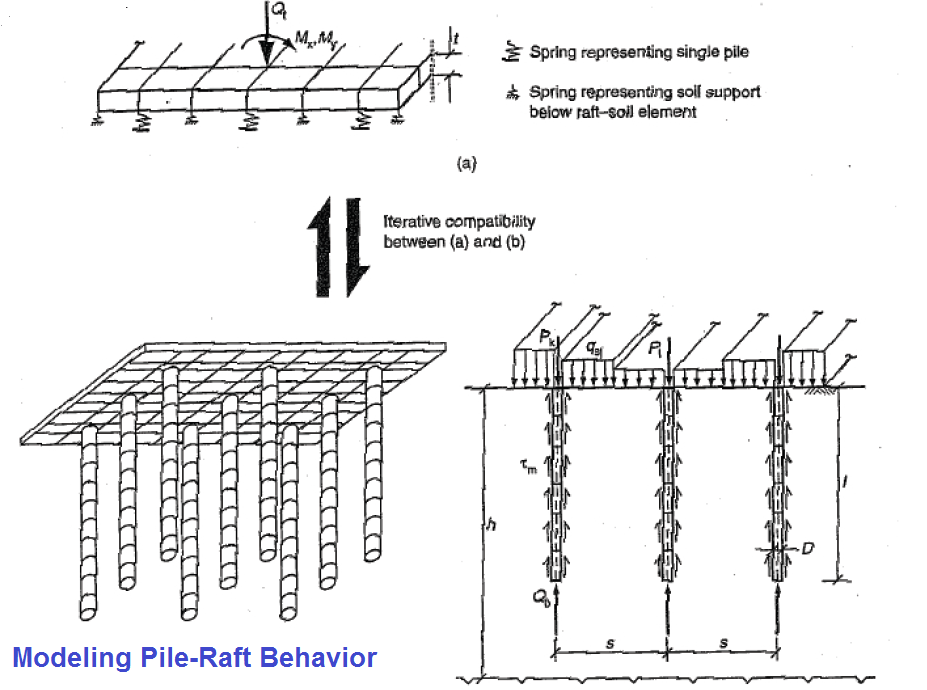
For the mat on foundation, information is available in technical literature on subgrade modulus. Plainly, the reaction of soil against the base of a foundation is dependent on the deflection of the foundation; therefore, the value of the subgrade modulus is not constant. For many problems of a mat on foundation, however, a constant value of subgrade modulus will lead to acceptable solutions because deflections in most cases are relatively small. The ability to compute the settlement of the mat at all points will allow the engineer to use judgment about the value of modulus being used and adjustment in the value can be made where indicated. The ability to study the influence of the various parameters that enter the problem give the engineer the chance to study an important soil-structure-interaction problem in detail.

Features

  • The program employs a well-established analytical solution for soil-structure interaction under static loading.
  • The program does not set a limit on the number of finite element meshes for modeling. Only the size of RAM in the user's computer will limit the available meshes. Available element types include 4-node linear elements, 8-node quadratic elements, and 9-node Lagrangian elements.
  • The soil is assumed to behave in the linear range, but the user may assign different values of subgrade stiffness at various locations around the foundation.
  • The user may input various concentrated loads at nodal points, distributed loads at any element, and uniform loads for an entire mat or slab.
  • An option to compute equivalent concentrated loads on a circular pattern. This option is useful to place concentrated loads from anchor bolts of a mountain plate on top of the foundation.
  • The user may specify a mat or slab with any shape. The program has the capability to generate automatically finite-element meshes for mats or slabs with rectangular shapes or circular shapes.
  • Ability to compute deformation and stresses of space orthotropic plates. Three common types covered are: uniform plates with orthopropic reinforcements, plate with orthotropic enhanced ribs, and plate with one way box section.
  • The program will display the layout of finite-element meshes with nodal numbers and element numbers.
  • The program accepts any consistent units in computations.
  • The program will generate contour graphics of slab deformation and stress distribution. The program will also provide plots for deformed and un-deformed finite-element meshes.
  • The program generates output data for each nodal point and finite element.
  • The Graphics menu contains quick observations of results contained in the output file.
  • The files of input data and output data are text based and may be directly accessed from within the GeoMat program, employing the user's preferred text editor or word processor.
  • A section cut option is available, which is a useful tool to plot deflection, bending moment, or stress components along one or more straight cut lines.
  • A well-documented manual is provided with the relevant theoretical background and guidance to input screens.