Examples
Pile foundation under axial and lateral loads
A three-dimensional model was used for predicting the
response of a single pile subjected to axial and lateral
loads. Perfect bonding between the pile and the soil was
assumed. The pile is 10 m long with a diameter of 0.5
m. The surrounded soil has a diameter of 12 m and a depth
of 16 m. Elastic behavior was assumed for
both the pile and soil with values of Young’s modulus of
2x107 kPa and 2x104 kPa,
respectively.
A three-dimensional model was used for predicting the
response of a single pile subjected to axial and lateral
loads. Perfect bonding between the pile and the soil was
assumed. The pile is 10 m long with a diameter of 0.5
m. The surrounded soil has a diameter of 12 m and a depth
of 16 m. Elastic behavior was assumed for
both the pile and soil with values of Young’s modulus of
2x107 kPa and 2x104 kPa,
respectively.
It is interesting to note that the finite-element model
allows the diameter and stiffness of the pile and the
stiffness of the soil to be modified as a function of
depth with little additional effort.
Under a lateral load of 216kN, the finiet-element
model predicts a deflection of 0.71 cm, while the
Poulos method estimates 0.8 cm (Ref. 2). Unlike the
axial case, in which 8-node linear elements were used,
27-node Lagrangian elements were used for the lateral
case in order to improve the predicion of the
behavior.
Circular Footing
An axisymmetric finite-element model as used to
analyze a smooth, circular, rigid plate on elastic
soil. The radius of the footing is assumed to be 1m,
while both the radius and depth of the soil are 4 m;
thus H/R=4. Elastic properties of the soil were:
E=2400 kPa and ν=0.2.
The rigid footing is subjected to a vertical load of
500 kN, and the finite-element model predicts a
settlement of 0.072 m. For a deeper soil (H/R=10),
the settlement was computed to be 0.095 m. The latter
is very close to the settlement estimated by an
analytical solution of about 0.10 m. (Ref. 3)
Capacity of a strip footing foundation
A two-dimensional finite element model under plane strain
conditions was used to estimate the bearing capacity of a
strip footing. The Mohr-Coulomb model was used in
representing the nonlinear behavior of the soil.
The elastic properties of the foundation were: E=30,000
psi and ν=0.3. The nonlinear parameters of the soil
were : cohesion, c=10 psi, and friction angle φ=20.
The finite-element model predicts the load capacity to be
equal to 185 psi. Terzaghi's collapse solution estimates
the capacity to be 175 psi (Ref 1).
Piled raft foundation
A five-story building on stiff clay in Urawa City is
modeled and analyzed using AMPS. This structure sits on a
piled raft foundation, comprised of twenty piles and a
rectangular pilecap. The load capacity and displacement
values at the pile heads have been reported for this
case. This example investigates the accuracy of the AMPS
output as compared to the reported results.
The 18.2m-long piles are placed in a four by four grid and
vary in diameter, from 0.7m to 0.8m. The pilecap
dimensions are 28m by 27m by 1m thick. The piles are
assumed embedded in the pilecap, and the entire assembly
is modeled as a composite. There are eight distinct soil
layers present in this case.
Results obtained from AMPs are shown in the figures below.
Notice the stress “rings” produced in the soil layers
around the piles.
Oil-storage tank at power plant
An oil-storage tank for a power plant was constructed with
reinforced-concrete in the early 1970’s. The underground
tank with a diameter of 134 ft and a height of 19.5 ft is
no longer in service. Plans for the tank show that there
are a total of 37 concrete columns equally spaced on the
foundation mat to support the roof slab. The columns have
a diameter of 20 in. and are reinforced longitudinally
with 6 No. 7 rebars. The roof slab is 9.75 inches in
thickness and was designed based on the behavior of
two-way flat slabs using square drop panels at the
columns. About 2 feet of fill covered by grass sits on
the roof slab. The foundation of the tank is a reinforced
concrete mat which is 15 inches in thickness in the
vicinity of each column, and is 7 inches in thickness
elsewhere. The tank is encircled with a reinforced
concrete wall, 15 inches in thickness.
Because of limitations of space at the site, a portion of
the new facilities is proposed to be seated on top of the
existing underground oil-storage tank. Engineers
proceeded to conduct an initial evaluation of the
stability of the tank structure by using a 3-dimensional,
finite-element (3-D FEM) model. The results of analyses
with the 3-D FEM suggested that the tank is capable to
support portions of a new substation after strengthening
the existing roof slab.
The final location of the transformers was at the south
end of the tank, creating an asymmetric loading condition.
To analyze this loading, the full tank model was used.
The dimensions of the transformer pads are 18 ft. long by
9 ft. wide by 3 ft. tall. The transformer equipment load
of 400 kips was distributed evenly across the top of the
transformer pads. The mesh size on the top of the tank
was made smaller for this analysis, in order to improve
the accuracy of the stress results.
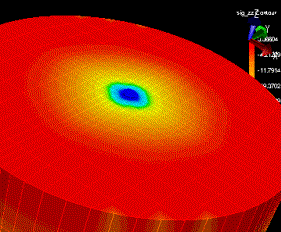
The maximum displacement in the tank slab is approximately
1/20 in. and is located at the interior corners of the
transformer pads. This result is reasonable, as these
corners are not underneath a column. The stress
distribution in the tank is shown Figures below. Half of
the tank has been cut away to reveal the stress in the
columns. The tank itself experiences an even
distribution; however the interior columns do not. Those
columns located nearest the transformers experience the
greatest amounts of stress.
References
- Chen and Baladi, Soil Plasticity, Elsevier, New
York, 1985.
- Trochanis, Bielak and Christiano, A
Three-Dimensional Nonlinear Study of Piles Leading to
the Development of a Simplified Model, Carnegie Mellon
University, Pittsburgh, 1988.
- Vermeer, PLAXIS, Tutorial Manual, A. A. Balkema,
Netherlands, 1991.
- Zienkiewicz and Taylor, The Finite Element Method,
McGraw Hill, England 1991.